Iterationsalgorithmus

5.3 Der Iterationsalgorithmus

Diese 3(k-2) diskretisierten Grundgleichungen ((5.2.1)-(5.2.3)), wobei k die Anzahl der Gitterpunkte ist, werden mittels eines Iterationsalgorithmus gelöst und dazu in die folgende Form gebracht:

0 = f_l,i (Ψ_i-1,φ_ni-1,φ_pi-1,Ψ_i,φ_ni,φ_pi, Ψ_i+1,φ_ni+1,φ_pi+1) (5.3.1)

l = 1 für die Poissongleichung,

l = 2 für die Kontinuitätsgleichung der Elektonen,

l = 3 für die Kontinuitätsgleichung der Löcher.

Die Lösung des Gleichungssystems erfolgt nach dem Newton- Raphson- Verfahren. An dieser Stelle erfolgt nur eine Darstellung der Grundzüge dieser Methode. Das Verfahren ist in [19] ausführlich beschrieben.

Entwickelt man Gleichung (5.3.1) in eine Taylorreihe und bricht diese Entwicklung nach dem linearen Glied ab, so erhält man:

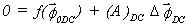
(A)_DC – Jacobi-Matrix,

der Index DC soll verdeutlichen das es sich um das Gleichungssystem für den statischen Fall handelt. Mit:

Ψ- Potential,

φ_n – Quasifermipotential der Elektronen,

φ_p – Quasifermipotential der Löcher.

Nachfolgend ist der Aufbau der Jacobi-Matrix dargestellt:

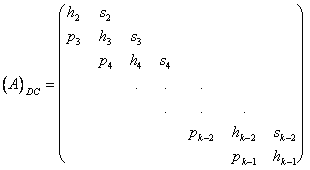
Die Funktionalmatrix besteht aus einer Hauptdiagonalen h und zwei Nebendiagonalen p, s. Derartige Gleichungssysteme erlauben es, den Rechenaufwand zum Bestimmen der Unbekannten erheblich zu verringern. Die allgemeine i-te Gleichung enthält nur die Unbekannten Δφ_i-1, Δφ_i und Δφ_i+1.

Der Lösungsalgorithmus

Selbst große tridiagonale Gleichungssysteme lassen sich mit dem Gaußschen Algorithmus in vertretbarer Zeit lösen. Weitergehende Ausführungen zum Lösungsalgorithmus sind in der Literatur (1) zu finden.

Die Elemente der Hauptdiagonale sind die Ableitungen der drei diskretisierten Halbleitergrundgleichungen an dem jeweiligen Gitterpunkt nach dem jeweiligen Potential:

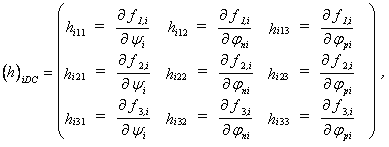
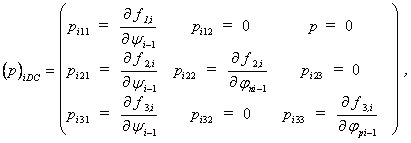
_{(1) H.R. Schwarz, “Numerische Mathematik”, Stuttgart, Teubner Verl., 1985}

Die Elemente p₁₂, p₁₃, p₂₃, p₃₂, s₁₂, s₁₃, s₂₃ und s₃₂ sind gleich Null, da in der Funktionalmatrix nur die Elemente besetzt sind, die partielle Ableitungen nach dem zentralen oder den beiden Nachbarpunkten besitzen.

Man beginnt bei der Berechnung mit einem Startvektor, dessen Elemente aus der Dotierung (1) oder aus der Lösung für einen anderen Arbeitspunkt bestimmt werden können. Man setzt den Startvektor in das Gleichungssystem (5.3.2) ein und stellt es nach dem Korrekturvektor Δφ_DC um. Anschließend wird dieser Korrekturvektor zur Startlösung addiert.

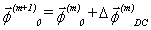
Φ₀(Ψ₀,φ_n0,φ_p0) – Startvektor,

Φ₀ ^(m+1) – verbesserte Lösung,

ΔΦ_DC – Korrekturvektor,

m – Iterationsschritt.

Auf diesem Weg erhält man eine verbesserte Lösung, mit Hilfe derer man das ursprüngliche Gleichungssystem (5.3.1) erneut lösen kann. Dabei erhält man wieder einen Korrekturvektor. Wiederholt wird dieser Vorgang solange bis der Korrekturvektor einem Abbruchkriterium (z.B. ε< 1×10^-1) genügt.

_{(1) M. Roßberg, “Kurzbeschreibung des Bauelementesimulators HETRA1”, Technische Hochschule Ilmenau, 1991}