5.7 Berechnung der y-Parameter
Als Ausgangspunkt für die Berechnung der y-Parameter dienen die Definitionsgleichungen (5.7.1) und (5.7.2). Mit deren Hilfe ist es möglich, das in Abbildung 3 dargestellte Kleinsignalersatzschaltbild aufzustellen:
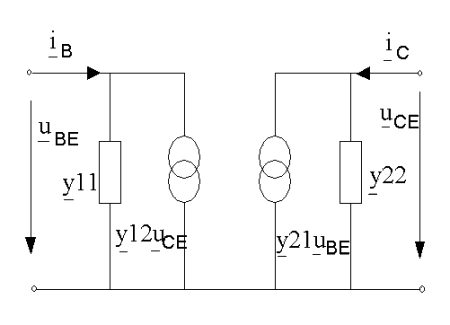
Abb. 3 Kleinsignalersatzschaltbild für die y-Parameter in Emitterschaltung
In der vorliegenden Arbeit wurden die folgenden Bestimmungsgleichungen für die Berechnung der Leitwertparameter zu Grunde gelegt:
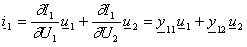
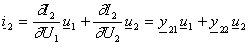
Für die y-Parameter wurden die Definitionsgleichungen (5.7.3) – (5.7.6) herangezogen:
(a) Eingangskurzschlußleitwert
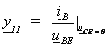
(b) Kurzschlußsteilheit
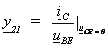
(c) Rückwirkungsleitwert
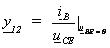
(d) Ausgangsleitwert
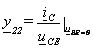
Für die Annahme (s. Kapitel 5.5), dass es sich bei den Kontakten um ideale ohmsche Kontakte in thermodynamischen Gleichgewicht handle, gelte die nachfolgende Beziehung. uBE stellt das Quasifermipotential der Löcher am Basiseinspeisungspunkt dar, uCE (z.B. uCE = 1xUT + 0xj) hingegen die aufgeprägte Kleinsignalspannung an der Kollektorseite (s.Kapitel 5.5). Zusätzlich zu den Größen des inneren Transistors wurden, zwecks der Vergleichbarkeit mit gemessenen Werten auch parasitäre Elemente berücksichtigt, insbesondere ein Basisbahnwiderstand am Eingang und ein Kollektorbahnwiderstand ausgangsseitig (s. Abbildung 4). Das hier verwendete eindimensionale Modell läßt nur eine Betrachtung der elektronisch aktiven Bereiche in dem Transistor zu. Nach der Berechnung der Kleinsignalkenngrößen wurden auch Elemente des inaktiven Bereiches in das Modell einbezogen. Das ermöglichte die Gegenüberstellung von gemessenen und simulierten Werten.
Eine Vergleichbarkeit war nötig, da anhand von gemessenen Werten die Gültigkeit des Modellkonzeptes sowie deren Implementierung in den Bauelementesimulator HETRA überprüft werden konnte. Die beiden Längswiderstände wurden in Vierpole überführt (Abb. 4), so entsteht eine Kettenschaltung von drei Vierpolen. Mittels der Multiplikation der a-Parametermatritzen (Kettenparameter) ist es möglich, die Parameter der Gesamtanordnung anzugeben (1). Die Ergebnisse der Berechnungen sind im Kapitel 6.1 beschrieben.
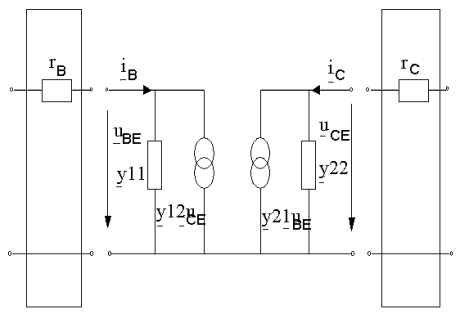
Abb. 4 Kleinsignalerstazschaltbild für die y-Parameter mit parasitären Elementen
(1) Phillipow, „Taschenbuch Elektrotechnik“, Berlin, Bd. 1, 3. Aufl.
