5 Das Modellkonzept
5.1 Ausgangspunkt
Als Ausgangspunkt für die theoretische Betrachtung im dynamischen Fall dient ein eindimensionales Modell zur Berechnung des statischen Verhaltens von SiGe- Heterobipolartransistoren. Deshalb wird zunächst das Modellkonzept für den statischen Fall näher beschrieben. Im Rahmen des Drift- Diffusionsmodells mußman im stationären Fall folgende Differentialgleichungen lösen:
(1) Poissongleichung
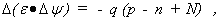
q-Elementarladung, ε – Dielektrizitätskonstante, Ψ – Potential, p -Löcherkonzentration, n – Elektronenkonzentration, N = ND – NA, ND – Donatorkonzentration, NA – Akzeptorkonzentration,
(2) Kontinuitätsgleichung der Elektronen
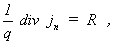
jn – Elektronenstromdichte,
R – Nettorekombinationsrate,
(2) Kontinuitätsgleichung der Löcher
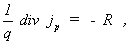
jp – Löcherstromdichte
Im Hinblick auf die rechentechnische Lösung dieses Differentialgleichungssystems ist die Einführung von Quasifermipotentialen für die Elektronen und die Löcher sinnvoll. Die Stromdichten erhalten folgende Form:
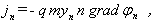
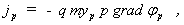
mit
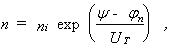
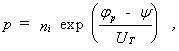
(Boltzmann- Näherung für Nichtentartung)
ni – Eigenleitungsdichte,
φn, φp – Quasifermipotential der Elektronen bzw. der Löcher,
μn, μp – Beweglichkeit der Elektronen bzw. der Löcher,
Ut – Temperaturspannung (Ut = 25,8 mV bei T = 300 K).
Bei einem Heterobipolartransistor kann man vom Dotierungs- und Germaniumgehalt abhängige Eigenleitungsdichten für Elektronen und Löcher einführen, um Hochdotierungseffekte und insbesondere den Heteroübergang zu beschreiben:
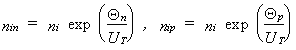
Θn,Θp – Bandparameter
Die Bandparameter Θn und Θp hängen nur vom Germaniumanteil ab. Sie beschreiben die relative Änderung der energetischen Lage von Leit- und Valenzbandkante und die Änderung der effektiven Zustandsdichten an den Bandkanten, bezogen auf Silizium ohne Germaniumanteil. Bei der Lösung des Gleichungssystems (5.1.1) – (5.1.3) muß man die Randbedingungen bei der Beschreibung des Basis-, Emitter- und Kollektoranschlusses beachten. Der Heteroübergang führt weiterhin zu einer ortsabhängigen Dielektrizitätskonstante ε. Diese Tatsache wirkt sich auf die Poissongleichung aus:
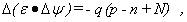
wobei ε jetzt eine Funktion des Germaniumanteils x und damit des Ortes ist,
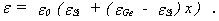
Eine ausführliche Erläuterung und eine mathematische Beschreibung der oben genannten Punkte, die bei der Modellierung von SiGe- Heterobipolartransistoren berücksichtigt werden müssen, ist in (1) gegeben.
(1) M. Roßberg, „Kurzbeschreibung des Bauelementesimulators HETRA1“, Technische Hochschule Ilmenau, 1991
